notes

《机器学习》第 1 章答案

Contents
  1. 1. 求版本空间
    1. 1.1. 题目
    2. 1.2. 分析
  2. 2. 估算可能假设的数目
    1. 2.1. 题目
    2. 2.2. 分析
    3. 2.3. 注意
  3. 3. 设计归纳偏好
    1. 3.1. 题目
    2. 3.2. 分析
  4. 4. 证明 NFL 定理
    1. 4.1. 题目
    2. 4.2. 分析
  5. 5. 机器学习在互联网搜索中的应用
    1. 5.1. 题目
    2. 5.2. 分析
  6. 6. References

本文为周志华《机器学习》第 1 章习题的试做答案，由于并没有标准答案，不保证所有题目答案的正确性。

求版本空间

题目

  • 西瓜数据集
编号色泽根蒂敲声好瓜
1青绿蜷缩浊响是
4乌黑稍蜷沉闷否

求相应的版本空间。

分析

参考书中 P5 图 1.2 ，不难得到本题数据集对应的版本空间如下：

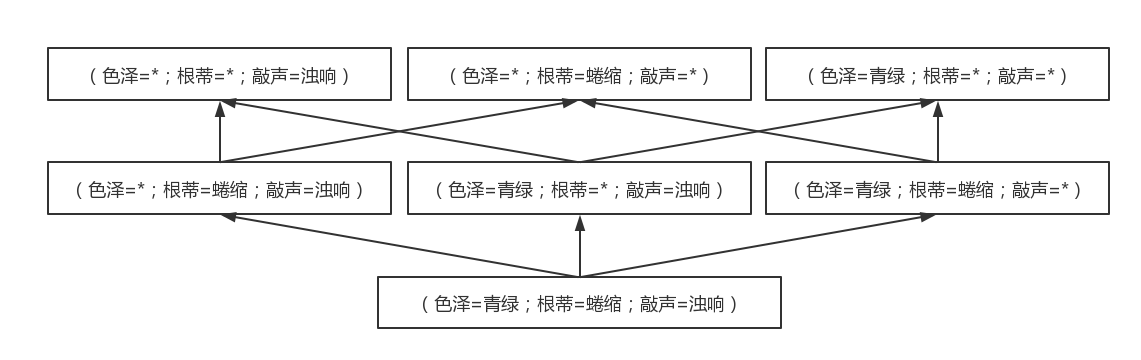
西瓜问题的版本空间

估算可能假设的数目

题目

  • 西瓜数据集
编号色泽根蒂敲声好瓜
1青绿蜷缩浊响是
2乌黑蜷缩浊响是
3青绿硬挺清脆否
4乌黑稍蜷沉闷否

与使用单个合取式来进行假设表示相比，使用 “析合范式” 将使得假设空间具有更强的表示能力 。例如：

好瓜↔⟮(色泽=∗) ∧ (根蒂=蜷缩) ∧ (敲声=∗)⟯ ∨ ⟮(色泽=乌黑) ∧ (根蒂=∗) ∧ (敲声=沉闷)⟯

会把 (色泽=青绿) ∧ (根蒂=蜷缩) ∧ (敲声=清脆) 以及 (色泽=乌黑) ∧ (根蒂=硬挺) ∧ (敲声=沉闷) 都分类为好瓜。若使用最多包含 kk 个合取式的析合范式来表达表中西瓜分类问题的假设空间，试估算共有多少种可能的假设。

分析

首先要理解 “假设空间的更强表示能力”： 若使用单个合取式，例如 (色泽=∗) ∧ (根蒂=蜷缩) ∧ (敲声=∗)，只代表根蒂蜷缩的瓜是好瓜。若采用上述析合范式，则其代表，除了根蒂蜷缩的瓜，乌黑沉闷的瓜也可以是好瓜。

对于色泽，有 33 种取值（青绿、乌黑、∗）；对于根蒂，有 44 种取值（蜷缩、硬挺、稍蜷、∗）；对于敲声，有 44 种取值（浊响、清脆、沉闷、∗）。由于表中训练集包含正例，因此排除 ∅\varnothing 的假设，那么单个合取式的假设空间规模大小为 3×4×4=483 \times 4 \times 4 = 48 。

如果将单个合取式的所有假设做析取，设取 kk 个合取式为一个析合范式，则假设空间规模大小为 C48kC_{48}^k ，但还需要注意冗余情况，例如 (A=a)∨(A=∗)(A=a) \vee (A=*) 与 (A=∗)(A=*) 等价。具体来说，

我们知道 (A∧B)∨(A∧C)=A∧(B∨C)(A \wedge B) \vee (A \wedge C) = A \wedge (B \vee C) ，则有：

1
⟮(色泽=青绿) ∧ (根蒂=蜷缩) ∧ (敲声=清脆)⟯ ∨ ⟮(色泽=青绿) ∧ (根蒂=蜷缩) ∧ (敲声=∗) ⟯ = ⟮(色泽=青绿) ∧ (根蒂=蜷缩)⟯ ∧ ⟮(敲声=清脆) ∨ (敲声=∗)⟯ = (色泽=青绿) ∧ (根蒂=蜷缩) ∧ (敲声=∗)

同理，

1
⟮(色泽=青绿) ∧ (根蒂=蜷缩) ∧ (敲声=沉闷)⟯ ∨ ⟮(色泽=青绿) ∧ (根蒂=蜷缩) ∧ (敲声=∗) ⟯ = (色泽=青绿) ∧ (根蒂=蜷缩) ∧ (敲声=∗)，

即出现了冗余。

理解题意：题中说，最多包含 kk 个合取式，如何理解其中的 “最多” 二字？显而易见，若将冗余项合并，假设空间中的每个析合范式未必具有同样个数的合取式，故 ”最多“ 指假设空间中析合范式中所含合取式个数的最大值。

故应考虑 kk 能够取到的最大值，不难推出，当一个析合范式包含了所有基本可能（不含泛化的合取式个数为 2×3×3=182 \times 3 \times 3 = 18）时，若再添加一个包含泛化的合取式，则合取式个数必会因为冗余消除而减少。故 kk 能够取到的最大值为 1818 。

当 k=18k = 18 时，估算假设空间的规模大小为：

∑i=118C18i\sum_{i = 1}^{18} C_{18}^i

故，若使用最多包含 1818 个合取式的析合范式来表达表中西瓜分类问题的假设空间，估算得共有 2182^{18} （218−12^{18} - 1） 种可能的假设。这个结论与网络上一些用程序跑出来的结果和使用真值表求解的结果一致。

注意

这里使用了基本可能的组合来代替泛化后的假设，实际上是可行的，例如包含 18 个合取式的析合范式实际等价于 (色泽=∗) ∧ (根蒂=∗) ∧ (敲声=∗) ，即泛化的假设都可以通过基本组合得出，故我们这里的估算是全面的。

有人认为假设空间规模应为 ∑i=148C48i\sum_{i = 1}^{48} C_{48}^i ，这是没有考虑到冗余的情况，书中明确提示了应该考虑冗余，而且根据我们的讨论，冗余的确会发生，故这种求法显然是错误的。

设计归纳偏好

题目

若数据包含噪声，则假设空间中可能不存在与所有训练样本都一致的假设。在此情形下，试设计一种归纳偏好用于假设选择。

分析

当数据包含噪声时，即，产生模型时，假设可以不只在版本空间中选取。这时我们应该如何在假设空间中作出选择呢？

可参考 kNN 法，做出如下归纳偏好：

  1. 每个属性都是同等重要的
  2. 属性相近的两个数据更类似
  3. 类似的数据归为同一类

证明 NFL 定理

题目

本章在论述 “没有免费的午餐” 定理时，默认使用了“分类错误率”作为性能度量来对分类器进行评估。若换用其他性能度量 ℓ\ell，则将改为：

Eote(La∣X,f)=∑h∑x∈(χ−X)P(x)ℓ(h(x),f(x))P(h∣X,La)E_{ote}(\mathfrak{L}_a | X,f) = \sum_h \sum_{x \in (\chi - \Chi)} P(x)\ell(h(x), f(x))P(h|X, \mathfrak{L}_a)

试证明 “没有免费的午餐定理” 仍成立。

分析

此题即证明 ∑fℓ(h(x),f(x))\sum_f \ell(h(x), f(x)) 与算法无关。由于 ff 均匀分布，则仍有一半的 ff 对 xx 的预测与 h(x)h(x) 不一致。新性能度量 ∑fℓ(h(x),f(x))\sum_f \ell(h(x), f(x)) 仍将是一个常数，故定理依然成立。

机器学习在互联网搜索中的应用

题目

试述机器学习在互联网搜索的哪些环节起什么作用。

分析

  1. 模式检测：阻止滥用和去除重复结果
  2. 相关推荐
  3. 图片搜索，理解图片内容

References

《机器学习》（周志华）第一章课后习题参考答案

机器学习(周志华) 参考答案 第一章 绪论 1.2

机器学习(周志华) 参考答案 第一章 绪论 题1.2

familyld/Machine_Learning

《机器学习》 周志华学习笔记第一章 绪论（课后习题）

P、NP、NPC 和 NP-Hard 相关概念的图形和解释

How Search Engines Use Machine Learning: 9 Things We Know for Sure

Mastodon